arviz_plots.plot_loo_pit

Contents

arviz_plots.plot_loo_pit#

arviz_plots.plot_loo_pit(dt, ci_prob=None, coverage=False, var_names=None, filter_vars=None, group='posterior_predictive', coords=None, sample_dims=None, plot_collection=None, backend=None, labeller=None, aes_by_visuals=None, visuals=None, stats=None, **pc_kwargs)[source]#

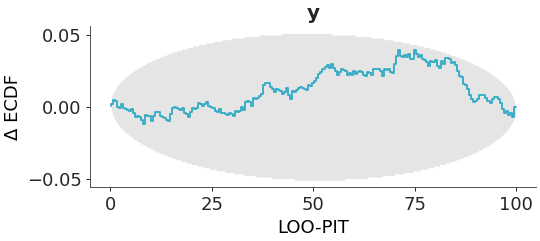
LOO-PIT Δ-ECDF values with simultaneous confidence envelope.

For a calibrated model the LOO Probability Integral Transform (PIT) values, $p(tilde{y}_i le y_i mid y_{-i})$, should be uniformly distributed. Where $y_i$ represents the observed data for index $i$ and $tilde y_i$ represents the posterior predictive sample at index $i$. $y_{-i}$ indicates we have left out the $i$-th observation. LOO-PIT values are computed using the PSIS-LOO-CV method described in [1] and [2].

This plot shows the empirical cumulative distribution function (ECDF) of the LOO-PIT values. To make the plot easier to interpret, we plot the Δ-ECDF, that is, the difference between the observed ECDF and the expected CDF. Simultaneous confidence bands are computed using the method described in described in [3].

Alternatively, we can visualize the coverage of the central posterior credible intervals by setting coverage=True. This allows us to assess whether the credible intervals includes the observed values. We can obtain the coverage of the central intervals from the LOO-PIT by replacing the LOO-PIT with two times the absolute difference between the LOO-PIT values and 0.5.

For more details on how to interpret this plot, see https://arviz-devs.github.io/EABM/Chapters/Prior_posterior_predictive_checks.html#pit-ecdfs.

Parameters:
dtxarray.DataTree

Input data

ci_probfloat, optional

Indicates the probability that should be contained within the plotted credible interval. Defaults to rcParams["stats.ci_prob"]

coveragebool, optional

If True, plot the coverage of the central posterior credible intervals. Defaults to False.

var_namesstr or list of str, optional

One or more variables to be plotted. Currently only one variable is supported. Prefix the variables by ~ when you want to exclude them from the plot.

filter_vars{None, “like”, “regex”}, optional, default=None

If None (default), interpret var_names as the real variables names. If “like”, interpret var_names as substrings of the real variables names. If “regex”, interpret var_names as regular expressions on the real variables names.

coordsdict, optional

Coordinates to plot.

sample_dimsstr or sequence of hashable, optional

Dimensions to reduce unless mapped to an aesthetic. Defaults to rcParams["data.sample_dims"]

plot_collectionPlotCollection, optional
backend{“matplotlib”, “bokeh”, “plotly”}, optional
labellerlabeller, optional
aes_by_visualsmapping of {strsequence of str}, optional

Mapping of visuals to aesthetics that should use their mapping in plot_collection when plotted. Valid keys are the same as for visuals.

visualsmapping of {strmapping or False}, optional

Valid keys are:

statsmapping, optional

Valid keys are:

  • ecdf_pit -> passed to ecdf_pit. Default is {"n_simulation": 1000}.

**pc_kwargs

Passed to arviz_plots.PlotCollection.grid

Returns:
PlotCollection

References

[1]

Vehtari et al. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing. 27(5) (2017) https://doi.org/10.1007/s11222-016-9696-4

[2]

Vehtari et al. Pareto Smoothed Importance Sampling. Journal of Machine Learning Research, 25(72) (2024) https://jmlr.org/papers/v25/19-556.html

[3]

Säilynoja et al. Graphical test for discrete uniformity and its applications in goodness-of-fit evaluation and multiple sample comparison. Statistics and Computing 32(32). (2022) https://doi.org/10.1007/s11222-022-10090-6

Examples

Plot the ecdf-PIT for the crabs hurdle-negative-binomial dataset.

>>> from arviz_plots import plot_loo_pit, style
>>> style.use("arviz-variat")
>>> from arviz_base import load_arviz_data
>>> dt = load_arviz_data('radon')
>>> plot_loo_pit(dt)
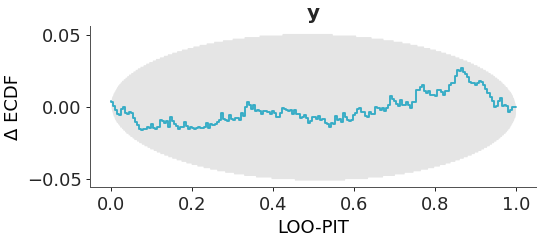
../../_images/arviz_plots-plot_loo_pit-1.png

Plot the coverage for the crabs hurdle-negative-binomial dataset.

>>> plot_loo_pit(dt, coverage=True)
../../_images/arviz_plots-plot_loo_pit-2.png

Plot of the probability integral transform of the posterior predictive distribution with respect to the observed data using the leave-one-out (LOO) method.

LOO-PIT ECDF

LOO-PIT ECDF
Contents